Además adjuntamos el archivo PDF para su descarga Descargar Aquí
Blog diseñado para la materia de Probabilidad y Estadística de la Facultad de Ingeniería de la UNAM. Grupo 12 de Probabilidad y Estadística, semestre 2014-1.
miércoles, 26 de febrero de 2014
Ejercicios Serie II
A continuación se presenta la resolución de 5 problemas de la Serie II, cuyo enlace es el siguiente Serie II, que a su vez se anexan dos ejercicios más resueltos en clase de la misma serie. Esperamos sea de su ayuda.
Además adjuntamos el archivo PDF para su descarga Descargar Aquí
Además adjuntamos el archivo PDF para su descarga Descargar Aquí
lunes, 24 de febrero de 2014
Vocabulario semana 4
(17 – 21 de Febrero del 2014)
Cardinalidad: En un
conjunto, la cardinalidad corresponde al número de elementos que tiene el
conjunto. (Ejemplo: Si el conjunto A se compone de tres elementos entonces la
cardinalidad del conjunto A se denota por: n(A)=3).
Conjunto: Un conjunto puede considerarse como una colección de
objetos, llamados miembros o elementos del conjunto. En general, mientras no se
especifique lo contrario, denotamos un conjunto por una letra mayúscula y un
elemento por una letra minúscula. Sinónimos de conjunto son clase, grupo y colección.
Un conjunto puede definirse
haciendo una lista de sus elementos o, si esto no es posible, describiendo
alguna propiedad conservada por todos los miembros y por los no miembros. El
primero se denomina el método de
extensión y el segundo el método de
comprensión.
Imagen tomada de http://www.fisicanet.com.ar/matematica/estadisticas/ap1/probabilidad05.gif
Contar: Numerar o
computar las cosas considerándolas como unidades homogéneas.
Conteo: En
probabilidad se considera al conteo como la técnica o conjunto de las mismas
que permiten establecer el número de resultados posibles de un experimento o una
combinación de ellos.
Espacio muestral: Se denomina espacio muestral (Ω) de un experimento
aleatorio al conjunto de todos los posibles resultados del mismo. Equivale al
conjunto de resultados donde puede ocurrir cualquier cosa:
Ω= {S1, S2, S3,
S4,…, Sn}
Puede ser:
-Finito:
Si el número de elementos que tiene Ω está acotado.
-Infinito
numerable: Cuando, a pesar de tener infinitos elementos, no siempre es
posible intercalar uno entre dos dados. (Ejemplo: El No de veces que hay que
lanzar un dado hasta que salga un 6, puede ser 5 o 6, pero nunca puede estar
entre 5 y 6, es decir, siempre será entero)
-Infinito
no numerable: Cuando Ω tiene infinitos elementos, y además siempre se puede
intercalar uno entre dos cualesquiera de ellos. (Ejemplo: Tiempo de espera
hasta que un paciente que acude a urgencias es atendido.)
Evento: Un evento
A, es un conjunto de posibles resultados del experimento. A es un subconjunto
de Ω (A ⊂
Ω).
Ejemplo:
Al tirar un dado hay n=6 resultados posibles. El espacio muestral es Ω= {ω1,
ω2, ω3, ω4, ω5, ω6}
donde ω1 es el evento de sacar un 1, ω2 es el evento de
sacar un 2 y así sucesivamente. Si definimos A como el evento de sacar un
número par, entonces A= { ω2, ω4, ω6}.
-Aleatorio: Un evento Aleatorio es aquel cuya
posibilidad de aparición no es totalmente conocida.
-Compuesto: Evento que
incluye dos o más eventos independientes.
-Determinista:
Los
fenómenos deterministas son aquellos en los cuales podemos adelantar resultados
basados en leyes que tienen modelos establecidos, como por ejemplo: caída libre
de un cuerpo que se lo puede determinar mediante fórmulas.
-Simple: Evento que
solo incluye un experimento del que se obtendrán los posibles resultados y
probabilidad de ocurra cada uno de ellos.
Imagen tomada de http://img67.imageshack.us/img67/3264/dados0137171vd6.jpg
Fenómeno: Toda
manifestación que se hace presente a la consciencia de un sujeto y aparece como
objeto de su percepción.
Probabilidad: La
probabilidad mide la frecuencia con la que se obtiene un resultado (o conjunto
de resultados) al llevar a cabo un experimento aleatorio, del que se conocen
todos los resultados posibles, bajo condiciones suficientemente estables
Fuentes:
·
Aprender y saber matemáticas, Introducción a la
Probabilidad, consultado el día 18 de febrero de 2014,
http://matematiesquinonez.blogspot.mx/2013/02/introduccion-la-probabilidad-eventos.html
·
Apuntes de Probabilidad y Estadística, Definiciones de
Probabilidad, archivo digital, consultado el día 18 de febrero de 2014,
http://www.upch.edu.pe/facien/fc/dbmbqf/zimic/ubioinfo/bks/Bioestadistica/estadistica%20descriptiva.pdf
·
Probabilidad, definiciones, archivo digital,
consultado el día 18 de febrero de 2014,
http://www.oikos.unam.mx/macroecologia/Curso_Estadistica/PROBABILIDAD.pdf
·
Probabilidad y Estadística, Técnicas de conteo,
consultado el día 18 de febrero de 2014,
http://probabilidadestadistic.blogspot.mx/2010/09/tecnicas-de-conteo.html
·
Profesor en línea, Cardinalidad de un conjunto,
consultado el día 18 de febrero de 2014
http://www.profesorenlinea.cl/quinto/matematica/ConjuntosCardinsalidad.htm
·
Real Academia Española, consultado el día 18 de
febrero de 2014,
http://lema.rae.es/drae/?val=contar
http://lema.rae.es/drae/?val=fenómeno
domingo, 16 de febrero de 2014
Pasos para la construcción de tablas de frecuencias
Pasos para la construcción de tablas de frecuencias
Las tablas de frecuencias son herramientas de Estadística,
siendo estas un resumen en forma de arreglo tabular de los datos útiles más que
una simple enumeración dada por medio de una recolección de datos. Este arreglo
tabular se forma por columnas en donde son colocados los datos estadísticos que
representan los distintos valores recogidos en la muestra y las frecuencias
(las veces) en que ocurren.
La mayor importancia de la elaboración de tablas de
frecuencias es la determinación del número de intervalos (clases) que la
conforman. Este número depende de la cantidad y de la naturaleza de los datos a
resumir asi como del fín que se busca con el resumen.
A continuación se presentan los
pasos recomendados a seguir para poder realizar una tabla de frecuencias. En
base a las fuentes consultadas, es posible que los primeros pasos se pueden
realizar en un orden diferente, más la que se presenta en actual trabajo se
apega más a un orden lógico.
I.- Recopilación de datos
Como la mayoría de los análisis estadísticos incluyen un
gran número de datos, con los cuales sería imposible utilizar para ciertos
fines si es que estos no son compactados por medio de un procedimiento conocido
como Tabla de Distribución de Frecuencias, siendo ésta la forma más común de
organiza un gran número de datos
Por lo anterior, la elaboración de la dicha tabla inicia
con la recopilación de datos. Esto consiste en escribir los datos de la muestra
que nos interesa conocer, sin tener un cierto orden. Es decir, los datos
obtenidos se depositan en algún documento.
Un ejemplo que servirá para explicar algunos puntos del
presente trabajo es el siguiente donde se presenta un cuadro con datos no
ordenados los cuales fueron obtenidos de una muestra de estudiantes a quienes
se les fue preguntada su estatura.
Cuadro I: “Obtención de datos no ordenados”
II.- Ordenamiento de los datos
Tras la obtención de los datos experimentales, y una vez
finalizada la etapa anterior, se procede a realizar un ordenamiento de datos.
Principalmente se busca ordenar los datos en forma
ascendente o descendente para facilitar el conteo de datos que correspondan a
cada uno de los intervalos a considerar
más adelante.
De esta forma, del ejemplo de las estaturas de los
estudiantes, una vez finalizada la encuesta, se procede a ordenarlos,
obteniendo la siguiente tabla:
Cuadro II: “ Datos obtenidos de manera ascendente”
III.- Rango de los datos (R)
Es conveniente realizar el cálculo
del rango de los datos obtenidos, con el fin de ser utilizado en los puntos
precedentes.
El rango se obtiene con la diferencia entre el dato mayor y el dato menor de la muestra.
IV.- Determinación del número
de clases (m)
Existen diversas formas para poder determinar el número de
clases, de manera que la elección de una de estas recae en el agrado y
comodidad del investigador
1.- El número de clases en que se agrupan los datos se
puede determinar como la raíz cuadrado del número de datos cuando este es menor
de 200. Para muestras con 200 o más datos el número de clases se determina con
la raíz cúbica del número de datos.
2.- Fórmula de Sturges (K): Esta forma sugiere la
utilización de la presente fórmula
Cabe mencionar que, si se decide
establecer previamente el tamaño o longitud longitud de clase , entonces el
número de clases se determina como
Algunas características
recomendadas son:
●
El número de clases debe ser entre 5 y 20, dependiendo
del rango y del número total de datos,aunque es mejor entre 7 y 10 clases.
●
Todos los datos deben estar incluidos en alguna clase.
De manera que siempre se redondea hacia arriba.
●
Hasta donde sea posible, debe omitirse trabajar tanto
con clases de anchos diferentes, como con clases abiertas.
V.- Cálculo del tamaño de
clase(c)
Tras obtener el número de clase con la que se trabajará,
se procede a determinar el tamaño o longitud de clase.
Para poder determinarlo, es necesario conocer previamente
el rango, como se mencionó anteriormente. Teniendo en cuenta esto, el tamaño de
clase se obtiene al dividir el rango entre el número de clases.
VI.- Rango de tabla
Una vez calculado el tamaño de clase y el número de clases
a trabajar, es importante antes de continuar con los demás pasos, obtener el
rango de tabla, siendo este un nuevo rango con el cual se obtendrán dos valores
llamados límites (en este caso superior e inferior) los cuales contienen a
todos nuestros datos obtenidos.
Al ser diferentes este rango (mayor) al rango obtenido previamente, es importante que abarque a todos los datos. Por lo tanto se buscará “centrar” el rango de tabla con el rango anterior, de manera, se debe obtener el cociente de la diferencia de los rangos y dos, y posteriormente sumar este cociente al dato máximo (Max xi), y a su vez restarselo al dato menor (Min xi).
Estos dos últimos números obtenidos representarán nuestros
límites aparentes, que a continuación explicaremos su importante función.
VII.- Elaboración de
intervalos y fronteras de clase (límites aparentes y reales)
Contando con el tamaño de clase, este último, nos indica
el número de datos que conforman a cada intervalo. Considerando los valores
extremos llamados límites. En cada intervalo aparece un límite inferior (LI) y
un límite superior (LS).
En este punto se deben realizar dos diferentes tipos de
intervalos, con diferentes tipos de límites. Estos son los Intervalos de clase,
los cuales incluye a los límites aparentes, y las Fronteras de clase, las
cuales incluye a los límites reales. Cabe destacar que para los pasos
siguientes, siempre se trabajara con los límites reales.
Como se vio en el punto anterior la obtención de los
límites aparentes, siendo estos números que se emplean para formar las clases. El
menor de ellos se llama límite Aparente inferior (LiA) y el mayor, el límite Aparente superior de la clase (LsA).
Para la obtención de los límites reales para las Frontera de clase, son aquellos que se obtienen retándole media unidad de medida al límite aparente inferior de una clase y sumándole media unidad de medida al límite superior aparente de las diferentes clases. El límite real inferior se denota como (LiR) y al límite superior real se le denota como (LsR).
Para determinar los valores de los límites para cada Frontera de clase, se le va adicionando de manera horizontal y vertical, el tamaño de clase, de manera que se logre coincidir, partiendo del límite inferior real menos una media unidad, con el valor del límite superior real menos una media unidad.
Para la obtención de los límites reales para las Frontera de clase, son aquellos que se obtienen retándole media unidad de medida al límite aparente inferior de una clase y sumándole media unidad de medida al límite superior aparente de las diferentes clases. El límite real inferior se denota como (LiR) y al límite superior real se le denota como (LsR).
Para determinar los valores de los límites para cada Frontera de clase, se le va adicionando de manera horizontal y vertical, el tamaño de clase, de manera que se logre coincidir, partiendo del límite inferior real menos una media unidad, con el valor del límite superior real menos una media unidad.
Para la determinación y elaboración de los Intervalos de
clase, cada intervalo se forma sumando al límite aparente inferior un número
menos que que el tamaño de clase para obtener así el límite real superior.
Tomando en cuenta los límites superior e inferior real, el límite real inferior con el cual se inicia es el valor redondeado hacia arriba, mientras
que para el límite aparente superior, es el valor redondeado hacia abajo.
La diferencia entre ambos es que, en los intervalos de
clase en donde se trabajan límites aparentes, siempre tendrán los mismos
dígitos significativos que los datos originales, además que el intervalo
superior es diferente al intervalo inferior inmediato de la siguiente clase.
Además de que la adición del tamaño de clase sólo es posible observar de manera
vertical. Por otro lado, en las fronteras de clase, en donde se trabajan
límites reales, se trabajan con números racionales (pudiendo ser también
los mismos dígitos significativos que
los datos originales), en donde el límite superior de un intervalo coincide con
el límite inferior de la clase siguiente, además de que la adición del tamaño
de clase se puede observar tanto vertical como horizontalmente.
La marca de clase o punto medio del intervalo es
simplemente es el cociente de la suma del límite inferior y superior real de
cada clase y dos. Es decir, para cada clase se trata del promedio de los
límites superior e inferior real. Se puede entender esto como el valor promedio
que se encuentra en cada clase, posteriormente se determinará su frecuencia
mediante un conteo.
IX.- Obtención de Frecuencias o conteo ( fi )
La frecuencia de clase se obtiene contando, en la tabla de
datos ordenados, los datos que correspondan al intervalo de dicha clase. Es
decir, en base a los límites de cada clase, se determina cuántos datos son
incluidos en esta clase, y este conteo representa nuestra Frecuencia.
X.- Frecuencia Acumulada( Fi )
La frecuencia acumulada, es la suma de la frecuencia de
clase y las frecuencias de las clases anteriores. Como es de esperarse, la
frecuencia acumulada de la primera clase es la misma frecuencia. Además, la
última frecuencia acumulada debe coincidir con el conteo total de datos de
nuestra tabla de datos ordenados inicial.
XI.- Frecuencia Relativa( f'i )
La frecuencia relativa, es el producto del cociente de la
frecuencia para cada clase y el total de datos (conteo) y cien, siendo esto un
porcentaje. Es decir, se trata de la
proporción de datos que se encuentran en cada clase.El multiplicarlo por cien
depende de la comodidad del investigador.
XII.- Frecuencia Relativa Acumulada( F'i)
La frecuencia relativa acumulada, es el cociente de la frecuencia acumulada (Fi) y el total de datos, el cual también se puede expresar como porcentaje. Es importante recalcar que la última Frecuencia Relativa Acumulada, debe representar la unidad o un 100%.
Una vez obtenidos estos datos, se concluye con la
construcción de la tabla de frecuencias, lo cual permite ahora calcular las
medidas descriptivas deseadas para un correcto análisis e interpretación de la
información de nuestros datos. De igual forma, es importante contar con una
representación gráfica de los datos de nuestra tabla de frecuencias.
El histograma de frecuencia, es un diagrama de barras que
representa, a escala, la frecuencia de las clases de una distribución de
frecuencias. Está formado por un conjunto de rectángulos, los cuales se
levanta uno para cada intervalo, de tal manera que la base será igual al tamaño
de clase ( C ) y la altura está dado, ya sea por la frecuencia , o también
la frecuencia acumulada ( en donde se ve
en esta última un crecimiento de izquierda a derecha).
Algunos ejemplos son:
Algunos ejemplos son:
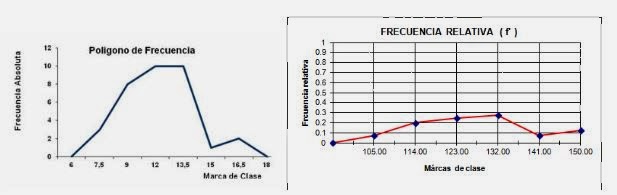
XIV.- Polígono de frecuencias.
Los vértices del Polígono son los puntos centrales de la
horizontal superior de cada barra del Histograma, es decir, las marcas de
clase.
Para cada valor de la variable corresponderá un valor de
la frecuencia señalando en el plano cartesiano por un punto; luego de
establecidos todos los puntos, se unen mediante líneas rectas, las que en
conjunto forman el polígono. Permite representar la frecuencia relativa como
también la frecuencia. Algunos ejemplos son:
Gráficos III y IV: “ Ejemplos de polígonos de
frecuencia y de frecuencia relativa”
XV.- Ojiva.
La Ojiva, es un gráfico que muestra las frecuencias
acumuladas menores que cualquier límite real superior de clase. Para el trazado
de esta gráfica, primeramente, se ubican los puntos en el plano cartesiano.
Dichos puntos se determinan teniendo en cuenta la marca de clase (eje x) y las
frecuencias absolutas o relativas acumuladas (eje y).
Gráficos IV y
V: “ Ejemplos de ojivas de frecuencia acumulada y frecuencia acumulada
relativa”
Es importante analizar las diferentes características que
presentan las curvas de frecuencia, en las que se pueden distinguir las
siguientes configuraciones:
Con esto también se busca dar a entender que, aun cuando
se tomen las medidas descriptivas comunes, es importante obtener algunas
medidas de forma de las curvas, ya que también permitirán obtener un mejor
análisis y comprensión del comportamiento de los datos.
Como se mencionó, la elaboración de una tabla de frecuencia, permite obtener las
medidas descriptivas para grupos de datos agrupados de una población o de una
muestra. Estas medidas nos proporcionará la información necesaria al
investigador para poder desarrollar conclusiones y observar el comportamiento e
información que emiten estos datos. A continuación se presenta una explicación
sucinta de estas medidas descriptivas con sus respectivas fórmulas.
Explicación Audio - Visual(material de refuerzo)
A continuación se proporcionan vídeos donde se explican
algunos de los elementos mencionados anteriormente o algunos conceptos necesarios
de antecedentes:
(Antecedentes)
●
“Frecuencia relativa y frecuencia relativa
acumulada”
Obtenido de : http://www.youtube.com/watch?v=ITc2GiZ0INg
●
“Frecuencia absoluta y frecuencia absoluta
acumulada”
(Repaso)
●
“Construcción de tablas de frecuencias y gráficas
estadísticas”
Obtenido de : http://www.youtube.com/watch?v=OzS7xkOUaE0
I.- Medidas de
tendencia central
Las medidas de tendencia central nos indican en torno a
qué valor (centro se distribuyen los datos).
Media
La media es el promedio de la distribución
Mediana
La mediana es la puntuación de la escala que separa la
mitad superior de la distribución y la inferior, es decir divide la serie de
datos en dos partes iguales (%50 de los datos abajo y 50% de los datos arriba).
Moda
Explicación Audio-Visual (material de refuerzo)
A continuación se proporcionan vídeos donde se explican
algunos de los elementos mencionados anteriormente o algunos conceptos
necesarios de antecedentes:
●
“Medidas de tendencia central. Moda, media y
mediana”
II.- Medidas de
Dispersión
Las medidas de dispersión nos informan sobre cuánto se
alejan del centro los valores de la distribución.
Rango
El rango es la diferencia entre el mayor y menor de los
datos de una distribución.
Varianza
La varianza es la media del cuadrado de las desviaciones
respecto a la media
Desviación media
La desviación media es la media de los valores absolutos
de las desviaciones respecto a la media.
Coeficiente de variación
Permite la comparación de la dispersión entre dos
poblaciones o muestras distintas e incluso, comprar la variación producto de dos
variables diferentes. Equivale a la razón entre la media y la desviación
estándar.
Explicación Audio-Visual (material de refuerzo)
A continuación se proporcionan vídeos donde se explican
algunos de los elementos mencionados anteriormente o algunos conceptos
necesarios de antecedentes:
● “Medidas de dispersión. Rango, desviación media,
varianza y desviación estándar”
Obtenido de : http://www.youtube.com/watch?v=ZTcUztM5UWs
III.- Medidas de
forma
Coeficiente de sesgo (Tercer momento
estandarizado)
Refleja el grado de simetría respecto de la media. Un
sesgo negativo da como resultado una cola de la gráfica asimétrica hacia los
valores pequeños de la variable, mientras que el sesgo positivo resulta en una
cola que se extiende hacia los valores grandes de la variable. Las variables
simétricas como las descritas por las distribuciones normal y uniforme, tienen
un sesgo igual a cero.
Imagen I: “Diferentes tipos de sesgos”
Coeficiente de curtosis
Describe lo puntiagudo de una distribución en
comparación con una distribución normal.
Es el grado de concentración que presenta los valores alrededores de la zona
central de distribución. Se definen tres tipos de distribuciones según grado de
curtosis:
-Distribución mesocúrtica: Grado de
concentración medio alrededor de los valores centrales de la variable (el mismo
que presenta una distribución normal). Coef. de Curtosis = 3
-Distribución Leptocúrtica: Presenta un elevado grado de
concentración alrededor de los valores centrales de la variable. Coef. de
Curtosis > 3
-Distribución Platicúrtica: Presenta un reducido grado de
concentración alrededor de los valores centrales de la variable. Coef. de Curtosis < 3
Imagen II: “Diferentes tipos de curtosis”
Explicación Audio-Visual (material de refuerzo)
A continuación se proporcionan videos donde se explican
algunos de los elementos mencionados anteriormente o algunos conceptos
necesarios de antecedentes:
●
“Medidas de la
Forma”
[Por cuestiones de Blogger, es imposible colocar el video http://youtu.be/SNllIAeD1SI , de igual manera recomendamos su consulta directa copiando el link en la barra de dirección web]
Obtenido de : http://www.youtube.com/watch?v=SNllIAeD1SI
IV.- Medidas de
forma
Cuantiles o Fractiles
Puntos tomados a intervalos regulares de la función de
distribución de una variable aleatoria. Su función es informar el valor de la
variable que ocupará la posición (en tanto por cien) que nos interese respecto
de todo el conjunto de variables. Los Cuantiles son unas medidas de posición
que dividen a la distribución en un cierto número de partes de manera que en
cada una de ellas hay el mismo de valores de la variable. Los más importantes
-Cuartiles: Dividen a la distribución en cuatro partes iguales (tres
divisiones). C1, C2, C3 correspondientes a 25%, 50% y 75%
-Deciles: Dividen a la distribución en 10 partes iguales (9
divisiones) D1, ..., D9 corresponden a 10%, ..., 90%
-Percentiles: Dividen a la distribución en 100 partes (99
divisiones) P1, ..., P99, correspondientes a 1%, ..., 99%
Existe un valor en cual coinciden los cuartiles, los
deciles y percentiles. Este es cuando son iguales a la Mediana.
De manera que los autores, buscan que quede una comprensión clara al estar revistando el presente trabajo, se agrega adicionalmente un pequeño ejemplo en Excel basado en los datos expuestos en el paso uno de la elaboración de una tabla de frecuencias. Se espera que sea de gran utilidad.
Basándose en los pasos planteados anteriormente, se
realizará un ejemplo en donde se muestre de manera clara como se deben elaborar
las tablas de frecuencias. Nos apoyaremos de Office Excel y se irá explicando paso a paso como se debe trabajar
en dicho programa para facilitar la elaboración de tablas.
Los datos obtenidos fueron en base a la
altura de algunos alumnos de una facultad.
1.- Recopilación de datos:
1.- Recopilación de datos:
Aquí se muestran los datos recopilados no ordenados de la altura de unos alumnos. Para hacer el análisis de una manera más sencilla y eficaz conviene ordenar los datos de menor a mayor, como se realizará a continuación, con el fin de poder identificar mucho más rápido las diferentes clases y marcas de clase.
2.- Ordenamiento de datos.
A continuación se muestra en primera instancia una tabla con los datos no ordenados y en seguida una con los datos ya ordenados:
Para realizar la tabla con los datos
ordenados en Excel, simplemente se tiene que buscar la opción Ordenar y
filtrar, y elegir las opciones que nos muestran como a se presenta a continuación:
3.- Obtención de Rango de datos:
Recordemos que el rango de datos se puede calcular de la siguiente manera:
Rango =Dato mayor-el dato menor
En el ejemplo, el rango quedaría de la siguiente manera:
Rango= 1.87 – 1.52 = 0.35
4.- Determinación del número de clases.
Como se mencionó anteriormente el número de clases se puede determinar con la raíz cuadrada de el número de datos, siempre y cuando esté último sea menor que 200, Por lo tanto lo determinaremos de esa manera.
Recordemos que el rango de datos se puede calcular de la siguiente manera:
Rango =Dato mayor-el dato menor
En el ejemplo, el rango quedaría de la siguiente manera:
Rango= 1.87 – 1.52 = 0.35
4.- Determinación del número de clases.
Como se mencionó anteriormente el número de clases se puede determinar con la raíz cuadrada de el número de datos, siempre y cuando esté último sea menor que 200, Por lo tanto lo determinaremos de esa manera.
5.- Cálculo de longitud de clases.
Basándonos en el número de clases, se calculara la longitud de las mismas, dividiendo el rango entre el número de clases. En el caso de que se obtenga un número con decimales, se decide redondear al número más cercano superior.
Basándonos en el número de clases, se calculara la longitud de las mismas, dividiendo el rango entre el número de clases. En el caso de que se obtenga un número con decimales, se decide redondear al número más cercano superior.
En la imagen anterior se puede observar el número de clases, y la longitud de clases.
6.- Rango de la tabla
Posteriormente se calcula el rango de la tabla, multiplicando el número de clases por el tamaño o longitud de las mismas.
Rango de tabla= 0.06 x 6 =0.36
Sabiendo el nuevo rango procederemos a centrar los datos según nuestro nuevo rango o rango de tabla. Utilizaremos la siguiente fórmula:
Para límite inferior.
7.-
Elaboración
de intervalos y fronteras de clase (límites aparentes y reales).
Cómo fue explicado en el trabajo, los límites reales o fronteras de clase se obtienen al centrar nuestros datos con el rango de la tabla. Y el límite real superior de la primera clase es exactamente igual al límite real inferior de la clase siguiente.
Cómo fue explicado en el trabajo, los límites reales o fronteras de clase se obtienen al centrar nuestros datos con el rango de la tabla. Y el límite real superior de la primera clase es exactamente igual al límite real inferior de la clase siguiente.
Los límites aparentes de los intervalos de clase tienen los mismos dígitos significativos que los datos originales. Y el aumento no va a ser de 0.06 como en el caso de las fronteras de clase, si no en 0.05. El aumento en este caso debe ser una unidad menor de cifras significativas en la longitud de las clases, ya que esta vez el límite superior aparente de una clase debe ser una unidad de cifra significativa menor que el límite inferior aparente de la clase siguiente.
Cabe destacar que nuestro primer límite aparente será de 0.005 unidades más que el primer límite real. Esto para que nuestros datos ajusten perfectamente.
Tomando en
cuenta los puntos anteriores nuestros límites reales y aparentes en nuestra
tabla quedan de la siguiente manera:
8.- Marcas de clase:
La marca de clase es el cociente de la suma del límite inferior y superior real (fronteras de clase) de cada clase y dos. Por lo tanto las marcas de clase quedan de la siguiente manera:
La marca de clase es el cociente de la suma del límite inferior y superior real (fronteras de clase) de cada clase y dos. Por lo tanto las marcas de clase quedan de la siguiente manera:
9.- Frecuencia
Al contar los datos ordenados de cada clase obtenemos nuestra tabla de frecuencia. Realizando un conteo de manera cuidadosa y observando que dichos datos se encontraran en su clase correspondiente, finalmente se obtuvo la siguiente tabla de frecuencia para cada clase. Lo anterior es posible realizarlo mediante una función de Excel mediante "tablas dinámicas"
Al contar los datos ordenados de cada clase obtenemos nuestra tabla de frecuencia. Realizando un conteo de manera cuidadosa y observando que dichos datos se encontraran en su clase correspondiente, finalmente se obtuvo la siguiente tabla de frecuencia para cada clase. Lo anterior es posible realizarlo mediante una función de Excel mediante "tablas dinámicas"
Explicación Audio-Visual (material de refuerzo)
En el siguiente vídeo, se muestra la obtención de frecuencias mediante tablas dinámicas, lo que es conveniente para el manejo de mayor numero de datos.
Obtenido de: www.youtube.com/watch?v=7zSM_VdaPr4
10.- Frecuencia acumulada
Para poder realizar tabla de frecuencia acumulada, se tiene que basar en la tabla de frecuencia.
De esta manera
se busca sumar la frecuencia de
cada clase y las frecuencias de las clases anteriores. La tablas de
frecuencia y frecuencia acumulada quedan de la siguiente manera:
11.- Frecuencia relativa
11.- Frecuencia relativa
Como ya se explico en el trabajo, la frecuencia relativa se obtiene por el producto del cociente de la frecuencia para cada clase y el total de datos. La frecuencia relativa en el ejemplo para cada clase es:
12.- Frecuencia relativa acumulada
La frecuencia relativa acumulada, se obtiene por la suma de la frecuencia relativa de cada clase (Calculada anteriormente) y la frecuencia relativa de las clases anteriores.
Nuestras tablas de frecuencia relativa y frecuencia relativa acumulada quedan de la siguiente de manera:
Al juntar cada pequeña tabla obtenemos nuestra tabla completa de datos agrupados y finalmente se concluye la elaboración de una tabla de frecuencias para los datos de la altura de los alumnos de una facultad.
Elaboración
de gráficas
I.
HISTOGRAMAS
a) Frecuencia
Para realizar
la gráfica de Marcas de clase vs. Frecuencia es necesario primero seleccionar
los datos de la frecuencia absoluta (que es con la que trabajamos para esta
gráfica) y hacer con ellos una gráfica de barras como se muestra a
continuación:

Una vez que se
tienen estos datos se puede modificar la gráfica para que quede en el eje de
las variables independientes los valores de las marcas de clase y así se puedan
observar los datos de forma más sencilla:
Seleccionamos
editar la serie y cambiamos el nombre y los valores en el eje X.
Quedando así la
gráfica:
Después vamos al
formato de punto de datos y seleccionamos un ancho de intervalo igual a cero y
en Color del borde seleccionamos un color distinto al de las barras para que se
distingan como barras y no sea una figura sólida.
Y por último damos
formato al eje X para determinar dónde están las marcas de agua y dónde las
fronteras, seleccionando una marca de graduación secundaria de tipo cruz y
damos nombre a los ejes, para que quede nuestra gráfica como deseamos.
Y queda nuestra
gráfica de la siguiente forma:
b) Frecuencia acumulada
Y haciendo lo mismo
pero con los valores de frecuencia acumulada (F) en lugar de la frecuencia
absoluta, quedando una gráfica como la siguiente:
I.Polígono de frecuencias
c) Frecuencia relativa
Para las gráficas
de polígonos en Excel seleccionamos la gráfica de dispersión donde los puntos
están unidos por lineas rectas. De nuevo seleccionamos los valores que irán en
el eje Y y damos formato a los valores en el eje X como a continuación se
muestra:
Primero agregamos
dos valores anteriores y uno posterior a lo que ya tenemos a las marcas de
clase y a la frecuencia relativa, al primero le restamos lo necesario para que
el intervalo con el primer número sea igual a los intervalos siguientes y al
del final le sumamos; al segundo le anteponemos un cero para que la gráfica
inicie en el orígen y le agregamos un cero al final para cerrar la gráfica y
poder obtener el área bajo la curva.
Luego seleccionamos
el tipo de gráfica con los valores en Y y modificamos como a las anteriores los
ejes, títulos de los mismos y título de la gráfica:
Para darle formato
a la gráfica, elegimos ver lineas verticales para que simule una cuadrícula:
Para que el gráfico
quede con las características que se desean, modificamos las opciones de del
eje X y colocamos en mínima el valor con el que queremos que empiecen los
valores en X:
Para finalizar agregamos títulos a los ejes y a la gráfica y colocamos las marcas de graduación principal y secundarias como en los histogramas:
d) OJIVA
Para la elaboración
de la Ojiva se siguen las mismas indicaciónes que para un polígono pero los
valores en el eje X son los de la frontera (límites inferiores) y en el eje Y
la frecuencia relativa acumulada, quedando de la siguiente forma la gráfica:
Comentario de los autores:
Los autores del presente trabajo esperan que mediante la teoría anteriormente presentada, y el presente trabajo, quede completamente asentado el aprendizaje para la elaboración de tablas de frecuencias. Es posible utilizar ciertos software (Excel) que permita un manejo y realización de operaciones, como también para la elaboración de gráficas, que como ya ce menciono, es de gran importancia para la estadística descriptiva.
Adjuntamos además el ejercicio en Excel para su consulta directa: http://www.mediafire.com/view/ds5zq8va3hauw39/Tablas_de_frecuencia_Ejemplo.xls
Agradecemos de su atención y esperamos que el presente trabajo sea de su agrado y consulta.
De antemano, aprovechamos para ofrecer unas disculpas respecto a ciertas imágenes que durante la edición virtual de este blog, no nos permiten acomodar de la manera más apropiada, de manera que estas se mueven un poco (acompañadas algunas de texto, causa también de ciertos espacios en blanco):
Fuentes:
●
HINES, William, et al, “Probabilidad y Estadística para
Ingeniería”, 4a edición, Patria, México, 2011
●
BORRAS, Hugo, et al, “Apuntes de Probabilidad y
Estadística”, Facultad de Ingeniería - UNAM, México, 1985
●
DEVORE, Jay L., “Probabilidad Y Estadística Para
Ingeniería Y Ciencias” , 5a edición, Thomson, México, 2008
●
Hernan Jaramillo. Frecuencia Absoluta y Frecuencia
Acumulada [en línea], ed.2013, Roberto Cuartas [Fecha de consulta:14 Febrero
2014]. Disponible en:
●
Ecured.Tablas de Frecuencias [en línea]. [Fecha de
Consulta: 14 de Febrero 2014]. Disponible en: <http://www.ecured.cu/index.php/Tablas_de_frecuencias>
●
Bioestadística Métodos y Aplicaciones(s.f). Consultado
el 14 de Frebrero 2014, de [http://www.bioestadistica.uma.es/baron/bioestadistica.pdf]
●
Arellano, Ruiz Beatriz (2011)Elaboración de una
Distribución de Frecuencias y sus Gráficas. Universidad Autonoma del Estado de
Hidalgo, http://www.uaeh.edu.mx/docencia/P_Presentaciones/prepa1/matematicas_elaboracion_de_una_distribucion_de_frecuencias.pdf.
●
Valdez y Alfaro Irene Patricia. Probabilidad y
Estadística. Division de Ciencias Básicas-Facultad de Ingeniería, UNAM, http://www.dcb.unam.mx/profesores/irene/Notas/regdifr.pdf
●
Lagos Gerardo (2013). Rango, tamaño, marca de clase,
distribución de frecuencia y límites reales de clase. Universidad Nacional de
Honduras, http://www.slideshare.net/Gerardo1977/intervalos-de-clase-estadstica
●
Mendez R. Ulises. ¿Como se construye una tabla de
Frecuencias?.UJED. http://bioestadisticaii.es.tl/%BFC%D3MO-SE-CONSTRUYE-UNA-TABLA-DE-FRECUENCIAS-f-.htm
●
Patricia. (2010). Construcción tablas de Frecuencia.
[Fecha de Consulta 14 Febrero 2014]. Disponible en: http://www.slideshare.net/patriciax/mc-pasos-construcciontablas-frecuencia
●
Valdez y Alfaro Irene Patricia. Probabilidad y
Estadística. División de Ciencias Básicas-Facultad de Ingeniería, UNAM. [Fecha
de consulta 14 Febrero 2014]. Disponible en: http://www.dcb.unam.mx/profesores/irene/EjerClase/EjercClas01.xls
●
Copyright Fundación Universitaria Inpahu (2012).
Distribución de Frecuencias.[Fecha de Consulta 15 Febrero 2014]. Disponible en:
http://www.inpahu.edu.co/tecnologias/Estadistica/distribucion.html
●
Vitutor (2012). Tablas de Frecuencia. [Fecha de
Consulta: 15 Febrero 2014] Disponible en: ]http://www.vitutor.com/estadistica/descriptiva/a_3.html
●
Valdez y Alfaro Irene Patricia. Probabilidad y
Estadística. División de Ciencias Básicas-Facultad de Ingeniería, Notas del
Curso, UNAM. [Fecha de consulta 15 Febrero 2014]. Disponible en:http://www.dcb.unam.mx/profesores/irene/Notas/esddes.pdf
●
Universidad Jaume I, “Medidad de centralizacion”,
Consultado el dua 10 de Febrero del 2014, Disponible enwww.uji.es/~mateu/Tema2-D37.doc
● "Oaca54","Coeficiente de variación", Consultado el día 30 de enero del 2014, http://www.slideshare.net/oaca54/coeficiente-de-variacin-13163623
● "Aula fácil", "Rango, varianza, desviación típica y coeficiente de variación", Consultado el día 30 de enero del 2014, www.aulafacil.com/CursoEstadistica/Lecc-6-est.htm
● Fundamentos de probabilidad", Consultado el día 30 de enero del 2014, http://www.dcb.unam.mx/users/gustavorb/Probabilidad/PE11.pdf
● Marín de la Fuente Yovana, "Distribución en probabilidad", Consultado el día 30 de de enero del 2014, http://www.slideshare.net/yovana93/tipos-de-12071948
● "Aula fácil", "Rango, varianza, desviación típica y coeficiente de variación", Consultado el día 30 de enero del 2014, www.aulafacil.com/CursoEstadistica/Lecc-6-est.htm
● Fundamentos de probabilidad", Consultado el día 30 de enero del 2014, http://www.dcb.unam.mx/users/gustavorb/Probabilidad/PE11.pdf
● Marín de la Fuente Yovana, "Distribución en probabilidad", Consultado el día 30 de de enero del 2014, http://www.slideshare.net/yovana93/tipos-de-12071948
Suscribirse a:
Comentarios (Atom)